Trisha Singh Mathematics Senior Thesis Presentation

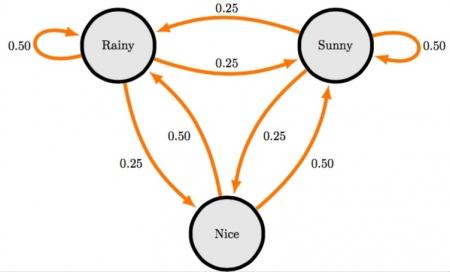
“Markov Chain Monte Carol Methods”: MCMC methods offer a solution to simulating from intractable probability distributions. By constructing a positive recurrent Markov chain that converges to the desired probability distribution, this method allows us to sample from the distribution. We examine why MCMC works, and how long it takes to converge. We start by exploring the Strong Law of Large Numbers for Markov chains, which explains how a constructed Markov chain can allow resampling from the desired probability distribution. We then examine the Metropolis Hastings algorithm, which is a mechanism for generating Markov chains for this purpose and explore some of its applications. Finally, we illustrate the rate of convergence of these Markov chains through an example.